Trigonométrie

Un triangle rectangle

La trigonométrie est la branche des mathématiques qui étudie le triangle et les rapports ente les côtés et les angles.

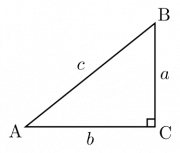
On définit tout d'abord les fonctions trigonométriques sur un triangle rectangle :

• Le sinus d'un angle est le rapport du côté opposé sur l'hypothénuse. On le note sin(x).
• Le sinus d'un angle est le rapport du côté adjacent sur l'hypothénuse. On le note cos(x).
• La tangente d'un angle est le rapport du côté opposé sur le côté adjacent. On le note tan(x).

Propriétés pour cette définition

sin(x) < 1                     (si 0 < x < 90) 

cos(x) < 1                     (si 0 < x < 90) 

(sin(x))<sup>2</sup> + (cos(x))<sup>2</sup> = 1

tan(x) = sin(x) : cos (x)

sin(x+y) = sin(x)cos(y) + cos(x)sin(y)

cos(x+y) = cos(x)cos(y) - sin(x)sin(y)

tan(x+y) = ( tan(x) + tan(y) ) : (1 - tan(x)tan(y))