« Parallélogramme » : différence entre les versions
« Parallélogramme » défini et expliqué aux enfants par les enfants.
Jump to navigation
Jump to search
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 1 : | Ligne 1 : | ||
[[Image:Parallélogramme.jpg|thumb|right]]Un '''parallélogramme''' est un [[Quadrilatère|quadrilatère]] dont les côtés opposés sont [[Parallélisme (géométrie)|parallèles]] deux à deux. |
|||
Un '''parallélogramme''' est une figure [[Géométrie|géométrique]]. |
|||
== Propriétés == |
|||
| ⚫ | |||
=== Caractéristiques === |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
#Si un quadrilatère est un parallélogramme, alors ses angles consécutifs sont supplémentaires. |
|||
#Si un quadrilatère est un parallélogramme, alors ses diagonales se coupent en leur milieu. |
|||
#Si un quadrilatère est un parallélogramme, alors il admet un centre de symétrie. |
|||
| ⚫ | |||
<br> |
|||
*ses côtés opposés sont de même longueur |
|||
== 6 propriétés qui prouvent qu'un quadrilatère est parallèlogramme == |
|||
*ses côtés opposés sont [[Parallélisme (géométrie)|parallèles]] |
|||
| ⚫ | |||
*ses angles consécutifs sont [[Angles supplémentaires|supplémentaires]] |
|||
*ses [[Diagonale|diagonales]] se coupent en leur milieu |
|||
*il admet un centre de [[Symétrie|symétrie]] : le point d'intersection de ses [[Diagonale|diagonales]] |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
#Si les angles opposés d'un quadrilatère sont de même mesure, alors c'est un parallélogramme. |
|||
| ⚫ | |||
#Si un quadrilatère admet un centre de symétrie, alors c'est un parallélogramme. |
|||
| ⚫ | |||
== Exemple == |
|||
| ⚫ | |||
*Si un quadrilatère (non croisé) a une paire de côtés opposés [[Parallélisme (géométrie)|parallèles]] et de même longueur alors ce quadrilatère est un parallélogramme. |
|||
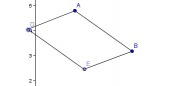
ABED est un parallélogramme. |
|||
| ⚫ | |||
| ⚫ | |||
<br> |
|||
| ⚫ | |||
[[Image:Parallélogramme.jpg|thumb|center]] |
|||
[[Catégorie:Mathématiques]] |
[[Catégorie:Mathématiques]] |
||
Version du 11 mars 2013 à 07:51
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux.
Propriétés
Caractéristiques
Si un quadrilatère est un parallélogramme alors :
- ses côtés opposés sont de même longueur
- ses côtés opposés sont parallèles
- ses angles opposés sont de même mesure
- ses angles consécutifs sont supplémentaires
- ses diagonales se coupent en leur milieu
- il admet un centre de symétrie : le point d'intersection de ses diagonales
Reconaissance d'un parallélogramme
- Si un quadrilatère (non croisé) a ses côtés opposés parallèles, alors c'est un parallélogramme.
- Si un quadrilatère (non croisé) a ses côtés opposés de même longueur, alors c'est un parallélogramme.
- Si un quadrilatère (non croisé) a une paire de côtés opposés parallèles et de même longueur alors ce quadrilatère est un parallélogramme.
- Si les diagonales d'un quadrilatère se coupent en leur milieu, alors c'est un parallélogramme.
- Si les angles opposés d'un quadrilatère sont de même mesure, alors c'est un parallélogramme.
- Si un quadrilatère admet un centre de symétrie, alors c'est un parallélogramme.






 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels