« Archimède » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 15 : | Ligne 15 : | ||
C'était aussi un génie dans le domaine de la [[Mécanique|mécanique]] pratique : ses machines de guerre ont permis de résister trois ans aux attaques des [[Rome antique|Romains]] à Syracuse. |
C'était aussi un génie dans le domaine de la [[Mécanique|mécanique]] pratique : ses machines de guerre ont permis de résister trois ans aux attaques des [[Rome antique|Romains]] à Syracuse. |
||
Archimède et l'approximation<br>du cercle |
Archimède et l'approximation<br>du cercle |
||
== <br>Sa plus grande recherche == |
== <br>Sa plus grande recherche == |
||
Archimède |
Archimède essaie de trouver le nombre ''pi''. Actuellement on ne l'a pas encore trouvé complètement (3,141592654...). |
||
=== Son raisonnement === |
=== Son raisonnement === |
||
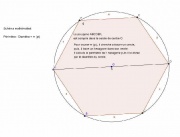
Pour trouver ce nombre, il commence par tracer un cercle. Ensuite, il trace un polygone dans son [[Cercle|cercle]] (un hexagone). ll cherche le [[Périmètre|périmètre]] de l[[Hexagone|'hexagone]] qui est proche du cercle. Après, il divise le périmètre par le [[ |
Pour trouver ce nombre, il commence par tracer un cercle. Ensuite, il trace un polygone dans son [[Cercle|cercle]] (un hexagone). ll cherche le [[Périmètre|périmètre]] de l[[Hexagone|'hexagone]] qui est proche du cercle. Après, il divise le périmètre par le [[Diametre|diamètre]]. Il trouve a peu près 3 + 10/71 = 3,1408... a peu près PI, ce qui n'est déjà pas trop mal pour les moyens de l'époque car il ne trouve qu'une valeur approchée. Pour être plus précis, il faut tracer un [[Polygone|polygone]] avec le plus de côtés égaux possible. |
||
[[Image: |
[[Image:Approximation du cercle.jpg|thumb|right]]<br> |
||
== Sa mort<br> == |
== Sa mort<br> == |
||
Les [[ |
Les [[Guerres puniques|guerres puniques]] opposèrent les Carthaginois (Phénicie) et la République romaine de 264 à 146 av. JC. Le siège de Syracuse s'est déroulé entre -213 et -212 et, pendant ce siège, Archimède créa les défenses de cette ville. Il fit déployer de nombreuses catapultes et inventa un système de miroirs métalliques géants, recouvert d'une mince couche de bronze poli. Le soleil, en se reflétant sur les miroirs, provoqua l'incendie des galères romaines. |
||
Les scientifiques et historiens sont sceptiques : il est peu vraisemblable qu'Archimède ait réussi cet exploit, et les sources sont fragiles. |
|||
La légende dit qu' Archimède aurait reçu un coup d'épée d'un soldat romain alors qu'il traçait des figures géométriques au sol. Il n'entendit pas le soldat arriver, parce qu'il était très concentré. Il avait 75 ans. <br> |
|||
== Références documentaires == |
== Références documentaires == |
||
| Ligne 40 : | Ligne 42 : | ||
*http://fr.wikipedia.org/wiki/Guerres_puniques |
*http://fr.wikipedia.org/wiki/Guerres_puniques |
||
[[ |
[[Catégorie:Ingénierie_et_métiers_de_l'ingénieur]] |
||
Version du 29 avril 2014 à 00:43
Archimède de Syracuse est un savant grec de l'antiquité, à la fois physicien et mathématicien. Il est né en -287 et mort en -212 à Syracuse.
Ses études, son enseignement
Archimède a étudié l'astronomie avec son père, à Syracuse, en Sicile, puis les mathématiques avec Conon de Samos, en Égypte, à l'école d'Alexandrie. Il a approfondi ses études une fois rentré chez lui à Syracuse.
Il a enseigné les mathématiques, la chimie et la physique, en Égypte, à l'école d'Alexandrie.
Ses découvertes
Archimède a apporté la perfection au système de numération grec en élaborant une méthode permettant d'exprimer les très grands nombres, le système d'Archimède, le système de levier, l'homme qui flotte...
Il a découvert les lois de la géométrie par rapport à la physique.
C'était aussi un génie dans le domaine de la mécanique pratique : ses machines de guerre ont permis de résister trois ans aux attaques des Romains à Syracuse.
Archimède et l'approximation
du cercle
Sa plus grande recherche
Archimède essaie de trouver le nombre pi. Actuellement on ne l'a pas encore trouvé complètement (3,141592654...).
Son raisonnement
Pour trouver ce nombre, il commence par tracer un cercle. Ensuite, il trace un polygone dans son cercle (un hexagone). ll cherche le périmètre de l'hexagone qui est proche du cercle. Après, il divise le périmètre par le diamètre. Il trouve a peu près 3 + 10/71 = 3,1408... a peu près PI, ce qui n'est déjà pas trop mal pour les moyens de l'époque car il ne trouve qu'une valeur approchée. Pour être plus précis, il faut tracer un polygone avec le plus de côtés égaux possible.
Sa mort
Les guerres puniques opposèrent les Carthaginois (Phénicie) et la République romaine de 264 à 146 av. JC. Le siège de Syracuse s'est déroulé entre -213 et -212 et, pendant ce siège, Archimède créa les défenses de cette ville. Il fit déployer de nombreuses catapultes et inventa un système de miroirs métalliques géants, recouvert d'une mince couche de bronze poli. Le soleil, en se reflétant sur les miroirs, provoqua l'incendie des galères romaines.
Les scientifiques et historiens sont sceptiques : il est peu vraisemblable qu'Archimède ait réussi cet exploit, et les sources sont fragiles.
La légende dit qu' Archimède aurait reçu un coup d'épée d'un soldat romain alors qu'il traçait des figures géométriques au sol. Il n'entendit pas le soldat arriver, parce qu'il était très concentré. Il avait 75 ans.
Références documentaires
- Universalis Junior, Paris, Encyclopédia Universalis, ISBN : 2-03-102331-4
- http://www.larousse.fr/encyclopedie/groupe-homonymes/guerres_puniques/139832
- Les guerres puniques.Arkéo junior 118[Périodique]. 01-04-2005. p.14-20.
- http://fr.wikipedia.org/wiki/Guerres_puniques







 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels