« Médiatrices dans un triangle » : différence entre les versions
m (a renommé Médiatrices dans des triangle en Médiatrices dans des triangles) |
Aucun résumé des modifications |
||
| (3 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
[[Image:Médiatrices.png|thumb|right]] |
|||
<u>''' Médiatrices dans un triangle:'''</u> |
|||
| ⚫ | |||
== Propriétés == |
|||
| ⚫ | |||
Les médiatrices sont concourantes dans le cas d'un [[triangle]]. Le point d'intersection de ces droites est le centre du cercle circonscrit du triangle (c'est-à-dire le seul point à [[équidistance]] de tous les sommets du triangle). |
|||
Par conséquent, pour trouver le centre du cercle circonscrit, il suffit de tracer deux des médiatrices. |
|||
| ⚫ | |||
== Remarque == |
|||
| ⚫ | |||
Dernière version du 10 décembre 2023 à 07:02
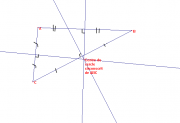
La médiatrice du côté d'un triangle est la droite qui passe par le milieu du côté et qui lui est perpendiculaire. Dans un triangle, on trouve trois médiatrices, une pour chaque côté.
Propriétés
Les médiatrices sont concourantes dans le cas d'un triangle. Le point d'intersection de ces droites est le centre du cercle circonscrit du triangle (c'est-à-dire le seul point à équidistance de tous les sommets du triangle).
Par conséquent, pour trouver le centre du cercle circonscrit, il suffit de tracer deux des médiatrices.
Remarque
Si le triangle contient un angle obtus (obtusangle) le centre du cercle circonscrit est hors du triangle et si tous les angles sont aigus (acutangle), alors le centre du cercle circonscrit est à l'intérieur du triangle.






 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels