« Théorème de Varignon » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| (19 versions intermédiaires par 7 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
Le '''théorème de Varignon''' regroupe plusieurs démonstrations de [[Pierre Varignon]] concernant le [[Quadrilatère|quadrilatère]] : |
|||
<u>'''Varignon'''</u> |
|||
#Si l'on joint les milieux des quatre cotés d'un [[Quadrilatère|quadrilatère]] quelconque, on obtient un [[Parallélogramme|parallélogramme]]. |
|||
Varignon Pierre était un géomètre français; il était aussi passionné par la physique. Il a vécu entre les 17éme et 18éme siécles. Il a réussi à démontrer que si on joint les milieux des cotés d'un quadrilatère, on obtient un parallélogramme, et si l'on procède de la même manière sur un carré on obtient un autre carré; cette règle s'appelle d'ailleurs le Théorème de Varignon. Il a grandi à Cean où il deviendra le sous dirrecteur d'une académie de recherche. Il a été nommé premier titulaire de Louis XIV. Il est mort en 1772. |
|||
#Si l'on joint les milieux des quatre cotés d'un [[Carré|carré]], on obtient un deuxième carré. |
|||
#Le périmètre du parallélogramme formé (voir 1 et 2) est égal à la somme des longueurs des deux diagonales du quadrilatère d'origine. |
|||
== Démonstrations == |
|||
=== Démontrer que EFGH est un parallélogramme === |
|||
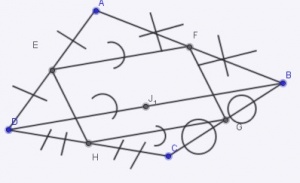
[[Image:Varignon.jpg|thumb|center|300px|Quadrilatère de Varignon]] |
|||
'''Étape 1 :'''<br> |
|||
Je sais que CBD est un triangle, H est le milieu de [DC], G est le milieu de [BC].<br> |
|||
''Or si dans un triangle, une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e.''<br> |
|||
Donc (BD) est parallèle à (HG). |
|||
'''Étape 2 :'''<br> |
|||
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].<br> |
|||
''Or si un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc EF est égal à DB/2 |
|||
'''Étape 3 :'''<br> |
|||
Je sais que (HG) est parallèle à (DB) et (DB) est parallèle à (EF).<br> |
|||
''Or si deux droites sont parallèles et qu'une 3e droite est parallèle à l'une d'elle, alors elle est aussi parallèle à l'autre.''<br> |
|||
Donc (HG) est parallèle à (EF). |
|||
'''Étape 4 :'''<br> |
|||
Je sais que DBC est un triangle, H est le milieu de [DC], G est le milieu de [BC].<br> |
|||
''Or si dans un triangle un segment joint les mileux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc HG = DB / 2 |
|||
'''Étape 5 :'''<br> |
|||
Je sais que ABD est un triangle, E est le milieu de [AD] et F est le milieu de [AB].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc EF = DB / 2 |
|||
Comme HG = DB / 2 et EF = DB / 2, alors HG = EF<br> |
|||
'''Étape 6 :'''<br> |
|||
Je sais que HG = EF et que (HG) est parallèle à (EF). |
|||
''Or si dans un quadrilatère 2 côtés opposés sont à la fois de même longueur et parallèles, alors c'est un parallèlogramme.'' |
|||
Donc IJKL est un parallélogramme. |
|||
=== Démontrer que le périmètre de EFGH est égal à la somme de AC et BD === |
|||
[[Image:Varignon.jpg|thumb|center|300px|Quadrilatère de Varignon]] |
|||
'''Étape 1 :'''<br> |
|||
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.''<br> |
|||
Donc EF = BD / 2<br> |
|||
'''Étape 2 :'''<br> |
|||
Je sais que CBD est un triangle, G est le milieu de [CD], H est le milieu de [CB].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc GH = BD / 2<br> |
|||
Comme EF = BD / 2 et GH = DB / 2, alors EF + GH = DB |
|||
'''Étape 3 :'''<br> |
|||
Je sais que ACD est un triangle, E est le milieu de [AB], H est le milieu de [DC].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtes, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc EH = AC / 2 |
|||
'''Étape 4 :'''<br> |
|||
Je sais que ACB est un triangle, F est le milieu de [AB], G est le milieu de [BC].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.''<br> |
|||
Donc FG = AC / 2<br> |
|||
Comme EH = AC / 2 et FG = AC / 2, alors EH + FG = AC |
|||
Comme EF + GH = DB et que EH + FG = AC |
|||
alors '''le périmètre de EFGH est égal à AC + DB''' |
|||
=== Démontrer que IJKL est un parallélogramme === |
|||
[[Image:Varignon.jpg|thumb|center|300px|Quadrilatère de Varignon]] |
|||
'''Étape 1 :''' |
|||
Je sais que I est le milieu de [AB], L est le milieu de [AD] et que ABD est un triangle. |
|||
''Or si dans un triangle une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e côté.'' |
|||
Donc (IL) est parallèle à (BD). |
|||
'''Étape 2 :''' |
|||
Je sais que CBD est un triangle, J est le milieu de [BC] et K est le milieu de [DC]. |
|||
''Or si dans un triangle une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e côté.'' |
|||
Donc (JK) est parallèle à (BD). |
|||
'''Étape 3 :''' |
|||
Je sais que (IL) est parallèle à (BD) et que (JK) est parall¨le à (BD). |
|||
''Or si deux droites sont parallèles à une même droite alors elles sont parallèles.'' |
|||
Donc (IL) est parallèle à (JK). |
|||
'''Étape 4 :''' |
|||
Je sais que I est le milieu de [AB], J est le milieu de [BC] et que ABC est un triangle. |
|||
''Or si dans un triangle une droite passe par les milieux de deux côtés alors elle est parallèle au troisième.'' |
|||
Donc (IJ) est parallèle à (AC). |
|||
'''Étape 5 :''' |
|||
Je sais que ADC est un triangle, Lest le milieu de [AD] et K est le milieu de [DC]. |
|||
''Or si dans un triangle une droite passe par les milieux de 2 côtés alors elle est parallèle au troisième.'' |
|||
Donc (LK) est parallèle à (AC). |
|||
'''Étape 6 :''' |
|||
Je sais que (LK) est paralèle à (AC) et que (IJ) est parallèle à (AC). |
|||
''Or si 2 droites sont parallèles à une même droite alors elles sont parallèles.'' |
|||
Donc (LK) est parallèle à (IJ). |
|||
'''Étape 7 :''' |
|||
Je sais que IJKL est un quadrilatère, (IL) est parallèle à (JK), (LK) est parallèle à (IJ). |
|||
''Or si dans un quadrilatère les côtés opposé sont parallèles alors c'est un parallélogramme.'' |
|||
Donc IJKL est un parallélogramme.<br> |
|||
== Voir aussi == |
|||
*[[Théorème|Théorème]] |
|||
*[[Pierre Varignon|Pierre Varignon]] |
|||
[[Catégorie:Mathématiques]] |
|||
Dernière version du 17 avril 2015 à 12:04
Le théorème de Varignon regroupe plusieurs démonstrations de Pierre Varignon concernant le quadrilatère :
- Si l'on joint les milieux des quatre cotés d'un quadrilatère quelconque, on obtient un parallélogramme.
- Si l'on joint les milieux des quatre cotés d'un carré, on obtient un deuxième carré.
- Le périmètre du parallélogramme formé (voir 1 et 2) est égal à la somme des longueurs des deux diagonales du quadrilatère d'origine.
Démonstrations
Démontrer que EFGH est un parallélogramme
Étape 1 :
Je sais que CBD est un triangle, H est le milieu de [DC], G est le milieu de [BC].
Or si dans un triangle, une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e.
Donc (BD) est parallèle à (HG).
Étape 2 :
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].
Or si un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc EF est égal à DB/2
Étape 3 :
Je sais que (HG) est parallèle à (DB) et (DB) est parallèle à (EF).
Or si deux droites sont parallèles et qu'une 3e droite est parallèle à l'une d'elle, alors elle est aussi parallèle à l'autre.
Donc (HG) est parallèle à (EF).
Étape 4 :
Je sais que DBC est un triangle, H est le milieu de [DC], G est le milieu de [BC].
Or si dans un triangle un segment joint les mileux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc HG = DB / 2
Étape 5 :
Je sais que ABD est un triangle, E est le milieu de [AD] et F est le milieu de [AB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc EF = DB / 2
Comme HG = DB / 2 et EF = DB / 2, alors HG = EF
Étape 6 :
Je sais que HG = EF et que (HG) est parallèle à (EF).
Or si dans un quadrilatère 2 côtés opposés sont à la fois de même longueur et parallèles, alors c'est un parallèlogramme.
Donc IJKL est un parallélogramme.
Démontrer que le périmètre de EFGH est égal à la somme de AC et BD
Étape 1 :
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.
Donc EF = BD / 2
Étape 2 :
Je sais que CBD est un triangle, G est le milieu de [CD], H est le milieu de [CB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc GH = BD / 2
Comme EF = BD / 2 et GH = DB / 2, alors EF + GH = DB
Étape 3 :
Je sais que ACD est un triangle, E est le milieu de [AB], H est le milieu de [DC].
Or si dans un triangle un segment joint les milieux de 2 côtes, alors il a pour longueur la moitié de celle du 3e côté.
Donc EH = AC / 2
Étape 4 :
Je sais que ACB est un triangle, F est le milieu de [AB], G est le milieu de [BC].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.
Donc FG = AC / 2
Comme EH = AC / 2 et FG = AC / 2, alors EH + FG = AC
Comme EF + GH = DB et que EH + FG = AC
alors le périmètre de EFGH est égal à AC + DB
Démontrer que IJKL est un parallélogramme
Étape 1 :
Je sais que I est le milieu de [AB], L est le milieu de [AD] et que ABD est un triangle.
Or si dans un triangle une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e côté.
Donc (IL) est parallèle à (BD).
Étape 2 :
Je sais que CBD est un triangle, J est le milieu de [BC] et K est le milieu de [DC].
Or si dans un triangle une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e côté.
Donc (JK) est parallèle à (BD).
Étape 3 :
Je sais que (IL) est parallèle à (BD) et que (JK) est parall¨le à (BD).
Or si deux droites sont parallèles à une même droite alors elles sont parallèles.
Donc (IL) est parallèle à (JK).
Étape 4 :
Je sais que I est le milieu de [AB], J est le milieu de [BC] et que ABC est un triangle.
Or si dans un triangle une droite passe par les milieux de deux côtés alors elle est parallèle au troisième.
Donc (IJ) est parallèle à (AC).
Étape 5 :
Je sais que ADC est un triangle, Lest le milieu de [AD] et K est le milieu de [DC].
Or si dans un triangle une droite passe par les milieux de 2 côtés alors elle est parallèle au troisième.
Donc (LK) est parallèle à (AC).
Étape 6 :
Je sais que (LK) est paralèle à (AC) et que (IJ) est parallèle à (AC).
Or si 2 droites sont parallèles à une même droite alors elles sont parallèles.
Donc (LK) est parallèle à (IJ).
Étape 7 :
Je sais que IJKL est un quadrilatère, (IL) est parallèle à (JK), (LK) est parallèle à (IJ).
Or si dans un quadrilatère les côtés opposé sont parallèles alors c'est un parallélogramme.
Donc IJKL est un parallélogramme.






 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels