« Théorème de Thalès » : différence entre les versions
« Théorème de Thalès » défini et expliqué aux enfants par les enfants.
Jump to navigation
Jump to search
m (a renommé Le Théorème de Thalès en Théorème de Thalès) |
Aucun résumé des modifications |
||
| Ligne 1 : | Ligne 1 : | ||
Le '''théorème de Thalès''' ou '''théorème d'intersection''' est un théorème de [[Géométrie|géométrie]] qui prouve que :[[Image:Capture.png|thumb|right]] Si dans un triangle ABC il y a D un point du segment [AB] , E un point du segment [AC] et que (DE) est parallèle à (BC), alors AD/AB = AE/AC = DE/BC. |
|||
{{À fusionner}} |
|||
[[Image:Capture.png|thumb|right]] |
|||
| ⚫ | Ce théorème a été prouvé par le mathématicien et philosophe grec [[Thalès de Milet|Thalès de Milet]] (environ 550 avant J.C.). Il y a une légende au sujet de ce mathématicien qui dit que Thalès aurait calculé la hauteur d'une des [[Pyramide de Khéops|pyramides de Khéops]] (regardez ici par exemple : http://fr.wikipedia.org/wiki/Pyramide_de_Kh%C3%A9ops) en mesurant la longueur de son ombre au sol et la longueur de l'ombre d'un bâton de hauteur donnée. |
||
== <u>''''' Le théorème de Thalès.'''''</u><u>'''''<br>'''''</u> == |
|||
*<u></u>Ce théorème repose sur la proportionnalité des côtés d'un triangle. |
|||
| ⚫ | |||
*Il sert à calculer des longueurs à condition d'avoir deux droites parallèles. |
|||
Le théorème de la droite des milieux est un cas particulier du théorème de Thalès. |
|||
[[Catégorie:Mathématiques]] |
|||
Dernière version du 27 décembre 2014 à 17:40
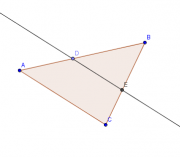
Le théorème de Thalès ou théorème d'intersection est un théorème de géométrie qui prouve que :
Si dans un triangle ABC il y a D un point du segment [AB] , E un point du segment [AC] et que (DE) est parallèle à (BC), alors AD/AB = AE/AC = DE/BC.
Ce théorème a été prouvé par le mathématicien et philosophe grec Thalès de Milet (environ 550 avant J.C.). Il y a une légende au sujet de ce mathématicien qui dit que Thalès aurait calculé la hauteur d'une des pyramides de Khéops (regardez ici par exemple : http://fr.wikipedia.org/wiki/Pyramide_de_Kh%C3%A9ops) en mesurant la longueur de son ombre au sol et la longueur de l'ombre d'un bâton de hauteur donnée.
- Ce théorème repose sur la proportionnalité des côtés d'un triangle.
- Il sert à calculer des longueurs à condition d'avoir deux droites parallèles.
Le théorème de la droite des milieux est un cas particulier du théorème de Thalès.
Ce que tu peux faire
Outils 
Outils personnels
