Parallélogramme

Un parallélogramme est une figure géométrique.

6 propriétés du parallélogramme

1. Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont parallèles.
2. Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont de même longueur.
3. Si un quadrilatère est un parallélogramme, alors ses angles opposés sont de même mesure.
4. Si un quadrilatère est un parallélogramme, alors ses angles consécutifs sont supplémentaires.
5. Si un quadrilatère est un parallélogramme, alors ses diagonales se coupent en leur milieu.
6. Si un quadrilatère est un parallélogramme, alors il admet un centre de symétrie.

6 propriétés qui prouvent qu'un quadrilatère est parallèlogramme

1. Si les côtés opposés d'un quadrilatère sont parallèles, alors c'est un parallélogramme.
2. Si les côtés opposés d'un quadrilatère sont de même longueur, alors c'est un parallélogramme.
3. Si les diagonales d'un quadrilatère se coupent en leur milieu, alors c'est un parallélogramme.
4. Si les angles opposés d'un quadrilatère sont de même mesure, alors c'est un parallélogramme.
5. Si deux côtés d'un quadrilatère sont à la fois de même longueur et parallèles, alors c'est un parallélogramme.
   
6. Si un quadrilatère admet un centre de symétrie, alors c'est un parallélogramme.

Exemple

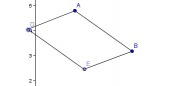
ABED est un parallélogramme.