« Théorème de Varignon » : différence entre les versions
m (a renommé Quadrilatère de Varignon en Théorème de Varignon) |
Aucun résumé des modifications |
||
| Ligne 1 : | Ligne 1 : | ||
Le ''' |
Le '''théorème de Varignon''' regroupe plusieurs démonstrations de [[Pierre Varignon]] concernant le [[Quadrilatère|quadrilatère]] : |
||
#Si l'on joint les milieux des quatre cotés d'un [[Quadrilatère|quadrilatère]] quelconque, on obtient un [[Parallélogramme|parallélogramme]]. |
#Si l'on joint les milieux des quatre cotés d'un [[Quadrilatère|quadrilatère]] quelconque, on obtient un [[Parallélogramme|parallélogramme]]. |
||
#Si l'on joint les milieux des quatre cotés d'un [[Carré|carré]], on obtient un deuxième carré. |
#Si l'on joint les milieux des quatre cotés d'un [[Carré|carré]], on obtient un deuxième carré. |
||
#Le périmètre du parallélogramme formé (voir 1 et 2) est égal à la somme des longueurs des deux diagonales du quadrilatère d'origine |
#Le périmètre du parallélogramme formé (voir 1 et 2) est égal à la somme des longueurs des deux diagonales du quadrilatère d'origine. |
||
== Démonstrations == |
== Démonstrations == |
||
| Ligne 9 : | Ligne 9 : | ||
=== Démontrer que EFGH est un parallélogramme === |
=== Démontrer que EFGH est un parallélogramme === |
||
| ⚫ | |||
| ⚫ | |||
'''Étape 1 :'''<br> |
|||
| ⚫ | |||
Je sais que |
Je sais que CBD est un triangle, H est le milieu de [DC], G est le milieu de [BC].<br> |
||
| ⚫ | |||
| ⚫ | |||
Donc (BD) est parallèle à (HG). |
|||
| ⚫ | |||
'''Étape 2 :'''<br> |
|||
| ⚫ | |||
Je sais que ABD est un triangle, E est le milieu de [AB], F est le milieu de [AD].<br> |
|||
| ⚫ | |||
| ⚫ | |||
<br> |
|||
Donc (EF) est parallèle à (DB) |
|||
| ⚫ | |||
'''Étape 3 :'''<br> |
|||
| ⚫ | |||
Je sais que (HG) est parall¨le à (DB) et (DB) est parallèle à (EF).<br> |
|||
''Or si deux droites sont parallèles et qu'une 3e droite est parallèle à l'une d'elle, alors elle est aussi parallèle à l'autre.''<br> |
|||
Donc (HG) est parallèle à (EF). |
|||
'''Étape 4 :'''<br> |
|||
Je sais que DBC est un triangle, H est le milieu de [DC], G est le milieu de [BC].<br> |
|||
| ⚫ | |||
| ⚫ | |||
'''Étape 5 :'''<br> |
|||
Je sais que ABD est un triangle, E est le milieu de [AD] et F est le milieu de [AB].<br> |
|||
| ⚫ | |||
Donc EF = DB / 2 |
|||
| ⚫ | |||
'''Étape 6 :'''<br> |
|||
| ⚫ | |||
| ⚫ | |||
Donc IJKL est un parallélogramme. |
Donc IJKL est un parallélogramme. |
||
| Ligne 33 : | Ligne 63 : | ||
=== Démontrer que le périmètre de EFGH est égal à la somme de AC et BD === |
=== Démontrer que le périmètre de EFGH est égal à la somme de AC et BD === |
||
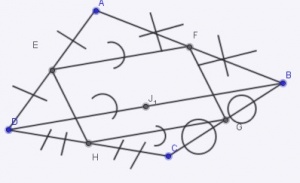
[[Image:Varignon.jpg|thumb|center|300px|Quadrilatère de Varignon]] |
|||
| ⚫ | |||
'''Étape 1 :'''<br> |
|||
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].<br> |
|||
| ⚫ | |||
Donc EF = BD / 2<br> |
|||
'''Étape 2 :'''<br> |
|||
Je sais que CBD est un triangle, G est le milieu de [CD], H est le milieu de [CB].<br> |
|||
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.''<br> |
|||
Donc GH = BD / 2<br> |
|||
| ⚫ | |||
'''Étape 3 :'''<br> |
|||
Je sais que ACD est un triangle, E est le milieu de [AB], H est le milieu de [DC].<br> |
|||
| ⚫ | |||
| ⚫ | |||
Donc EH = AC / 2 |
|||
étape 3 : Je sais que ACD triangle, E milieu [AB], H milieu [DC].<br>Or si dans un triangle un segment joint les milieux de |
|||
'''Étape 4 :'''<br> |
|||
| ⚫ | |||
Je sais que ACB est un triangle, F est le milieu de [AB], G est le milieu de [BC].<br> |
|||
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté. |
''Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.''<br> |
||
Donc FG=AC/ |
Donc FG = AC / 2<br> |
||
Comme EH=AC/ |
Comme EH = AC / 2 et FG = AC / 2, alors EH + FG = AC |
||
Comme EF+GH=DB et que EH+FG= |
Comme EF + GH = DB et que EH + FG = AC |
||
alors '''le périmètre de EFGH est égal à AC+DB''' |
alors '''le périmètre de EFGH est égal à AC + DB''' |
||
Voir aussi<br> == |
|||
*[[Théorème|Théorème]] |
|||
| ⚫ | |||
*[[Pierre Varignon|Pierre Varignon |
|||
[[Catégorie:Mathématiques]] |
[[Catégorie:Mathématiques]] |
||
Version du 14 avril 2013 à 14:56
Le théorème de Varignon regroupe plusieurs démonstrations de Pierre Varignon concernant le quadrilatère :
- Si l'on joint les milieux des quatre cotés d'un quadrilatère quelconque, on obtient un parallélogramme.
- Si l'on joint les milieux des quatre cotés d'un carré, on obtient un deuxième carré.
- Le périmètre du parallélogramme formé (voir 1 et 2) est égal à la somme des longueurs des deux diagonales du quadrilatère d'origine.
Démonstrations
Démontrer que EFGH est un parallélogramme
Étape 1 :
Je sais que CBD est un triangle, H est le milieu de [DC], G est le milieu de [BC].
Or si dans un triangle, une droite passe par les milieux de 2 côtés, alors elle est parallèle au 3e.
Donc (BD) est parallèle à (HG).
Étape 2 :
Je sais que ABD est un triangle, E est le milieu de [AB], F est le milieu de [AD].
Or si un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc (EF) est parallèle à (DB)
Étape 3 :
Je sais que (HG) est parall¨le à (DB) et (DB) est parallèle à (EF).
Or si deux droites sont parallèles et qu'une 3e droite est parallèle à l'une d'elle, alors elle est aussi parallèle à l'autre.
Donc (HG) est parallèle à (EF).
Étape 4 :
Je sais que DBC est un triangle, H est le milieu de [DC], G est le milieu de [BC].
Or si dans un triangle un segment joint les mileux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc HG = DB / 2
Étape 5 :
Je sais que ABD est un triangle, E est le milieu de [AD] et F est le milieu de [AB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc EF = DB / 2
Comme HG = DB / 2 et EF = DB / 2, alors HG = EF
Étape 6 :
Je sais que HG = EF et que (HG) est parallèle à (EF).
Or si dans un quadrilatère 2 côtés opposés sont à la fois de même longueur et parallèles, alors c'est un parallèlogramme.
Donc IJKL est un parallélogramme.
Démontrer que le périmètre de EFGH est égal à la somme de AC et BD
Étape 1 :
Je sais que ABD est un triangle, E est le milieu de [AD], F est le milieu de [AB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.
Donc EF = BD / 2
Étape 2 :
Je sais que CBD est un triangle, G est le milieu de [CD], H est le milieu de [CB].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié de celle du 3e côté.
Donc GH = BD / 2
Comme EF = BD / 2 et GH = DB / 2, alors EF + GH = DB
Étape 3 :
Je sais que ACD est un triangle, E est le milieu de [AB], H est le milieu de [DC].
Or si dans un triangle un segment joint les milieux de 2 côtes, alors il a pour longueur la moitié de celle du 3e côté.
Donc EH = AC / 2
Étape 4 :
Je sais que ACB est un triangle, F est le milieu de [AB], G est le milieu de [BC].
Or si dans un triangle un segment joint les milieux de 2 côtés, alors il a pour longueur la moitié du 3e côté.
Donc FG = AC / 2
Comme EH = AC / 2 et FG = AC / 2, alors EH + FG = AC
Comme EF + GH = DB et que EH + FG = AC
alors le périmètre de EFGH est égal à AC + DB
Voir aussi
==
- Théorème
- [[Pierre Varignon|Pierre Varignon






 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels