« Puissance (mathématiques) » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 1 : | Ligne 1 : | ||
La '''''puissance''''', en [[Mathématiques|mathématiques]], est représentée par a<sup>n </sup>qui est |
La '''''puissance'''''d'un nombre a, en [[Mathématiques|mathématiques]], est représentée par a<sup>n</sup> (où n est un nombre entier)<sup> </sup>qui est égale à : |
||
[[Image:Capturepui.PNG|left]]<br> |
[[Image:Capturepui.PNG|left]]<br> |
||
<br> |
<br> |
||
Ici, a s'appelle la '''base''' et n '''l'exposant'''. |
|||
<br> |
|||
<span> </span> Quand on fait la factorisation première d'un nombre, on utilise souvent des puissances. |
<span> </span> Quand on fait la factorisation première d'un nombre, on utilise souvent des puissances. |
||
Un nombre |
Un nombre à la puissance 0 est toujours égal à zéro, un nombre à la puissance 1 est toujours égal à lui-même. Un nombre à la puissance 2 est aussi appelé "au carré" (6² = 6x6 = 6 au carré) et un nombre à la puissance 3 est parfois appelé "au cube" (2<sup>3</sup> = 2x2x2 = 2 au cube). Les mesures de volume ou de surface utilisent également les puissances ([[Mètre carré|m²]], [[Mètre cube|m³]]).<br> |
||
<br> |
<br> |
||
| Ligne 23 : | Ligne 23 : | ||
== Les puissance de 10 et les écritures scientifiques == |
== Les puissance de 10 et les écritures scientifiques == |
||
Les puissance de 10 et les écritures scientifiques sont utilisées pour éviter d'écrire des nombres très grands ou très petits. |
|||
<u>puissances de 10 :</u> |
<u>puissances de 10 :</u> |
||
| Ligne 63 : | Ligne 63 : | ||
<br> |
<br> |
||
== Les puissances |
== Les puissances négatives == |
||
Soit a un nombre non nul et n un nombre entier. Le nombre a<sup>-n</sup>,dit "a exposant moins n",est l'inverse de la puissance de a :<sub></sub> |
Soit a un nombre non nul et n un nombre entier. Le nombre a<sup>-n</sup>,dit "a exposant moins n",est l'inverse de la puissance de a :<sub></sub> |
||
Version du 16 avril 2014 à 10:52
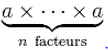
La puissanced'un nombre a, en mathématiques, est représentée par an (où n est un nombre entier) qui est égale à :
Ici, a s'appelle la base et n l'exposant.
Quand on fait la factorisation première d'un nombre, on utilise souvent des puissances.
Un nombre à la puissance 0 est toujours égal à zéro, un nombre à la puissance 1 est toujours égal à lui-même. Un nombre à la puissance 2 est aussi appelé "au carré" (6² = 6x6 = 6 au carré) et un nombre à la puissance 3 est parfois appelé "au cube" (23 = 2x2x2 = 2 au cube). Les mesures de volume ou de surface utilisent également les puissances (m², m³).
Calculer une puissance
- 50 = 1
- 51 = 5
- 52 = 5 x 5 = 25
- 53 = 5 x 5 x 5 = 125
- 54 = 5 x 5 x 5 x 5 = 625
Les puissance de 10 et les écritures scientifiques
Les puissance de 10 et les écritures scientifiques sont utilisées pour éviter d'écrire des nombres très grands ou très petits.
puissances de 10 :
Ecritures scientfiques : Ce sont les nombres qui peuvent s'écrire sous la forme de a*10n à condition que n est un entier, et a entre 1 et 10 :
Exemples :
Les puissances négatives
Soit a un nombre non nul et n un nombre entier. Le nombre a-n,dit "a exposant moins n",est l'inverse de la puissance de a :
a-n=1/an
On peut appliquer cette règle avec les exposants positifs :
an=1/a-n
Les cas particuliers
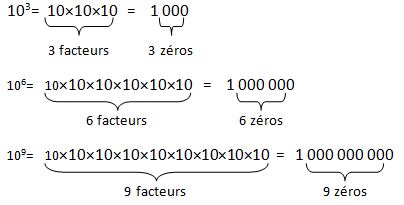
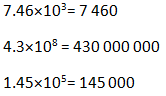








 Ce que tu peux faire
Ce que tu peux faire

 Outils
Outils 




 Outils personnels
Outils personnels